Parameter Importance
This panel surfaces which of your hyperparameters were the best predictors of, and highly correlated to desirable values of your metrics.

Correlation is the linear correlation between the hyperparameter and the chosen metric (in this case val_loss). So a high correlation means that when the hyperparameter has a higher value, the metric also has higher values and vice versa. Correlation is a great metric to look at but it can’t capture second order interactions between inputs and it can get messy to compare inputs with wildly different ranges.
Therefore we also calculate an importance metric where we train a random forest with the hyperparameters as inputs and the metric as the target output and report the feature importance values for the random forest.
The idea for this technique was inspired by a conversation with Jeremy Howard who has pioneered the use of random forest feature importances to explore hyperparameter spaces at Fast.ai. We highly recommend you check out his phenomenal lecture (and these notes) to learn more about the motivation behind this analysis.
This hyperparameter importance panel untangles the complicated interactions between highly correlated hyperparameters. In doing so, it helps you fine tune your hyperparameter searches by showing you which of your hyperparameters matter the most in terms of predicting model performance.
Creating A Hyperparameter Importance Panel
Go to your W&B Project. If you don’t have one, you can use this project.
From your project page, click Add Visualization.

Then choose Parameter Importance.
You don’t need to write any new code, other than integrating W&B into your project.

If an empty panel appears, make sure that your runs are ungrouped
Using the Hyperparameter Importance Panel
We can let wandb visualize the most useful set of hyperparameters by clicking on the magic wand beside the parameters manager. We can then sort the hyperparameters based on the Importance.
With the parameter manager, we can manually set the visible and hidden parameters.
Interpreting A Hyperparameter Importance Panel

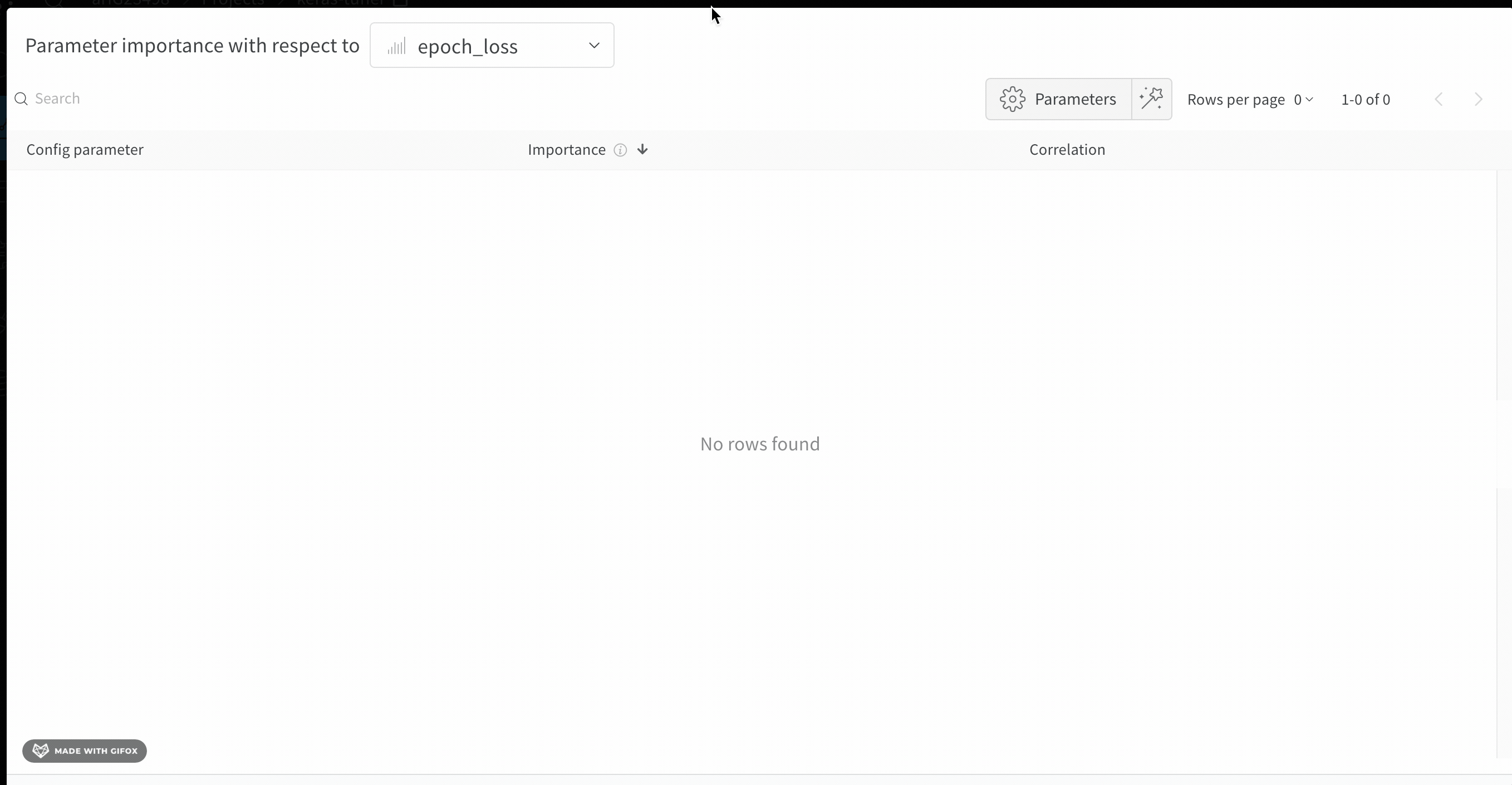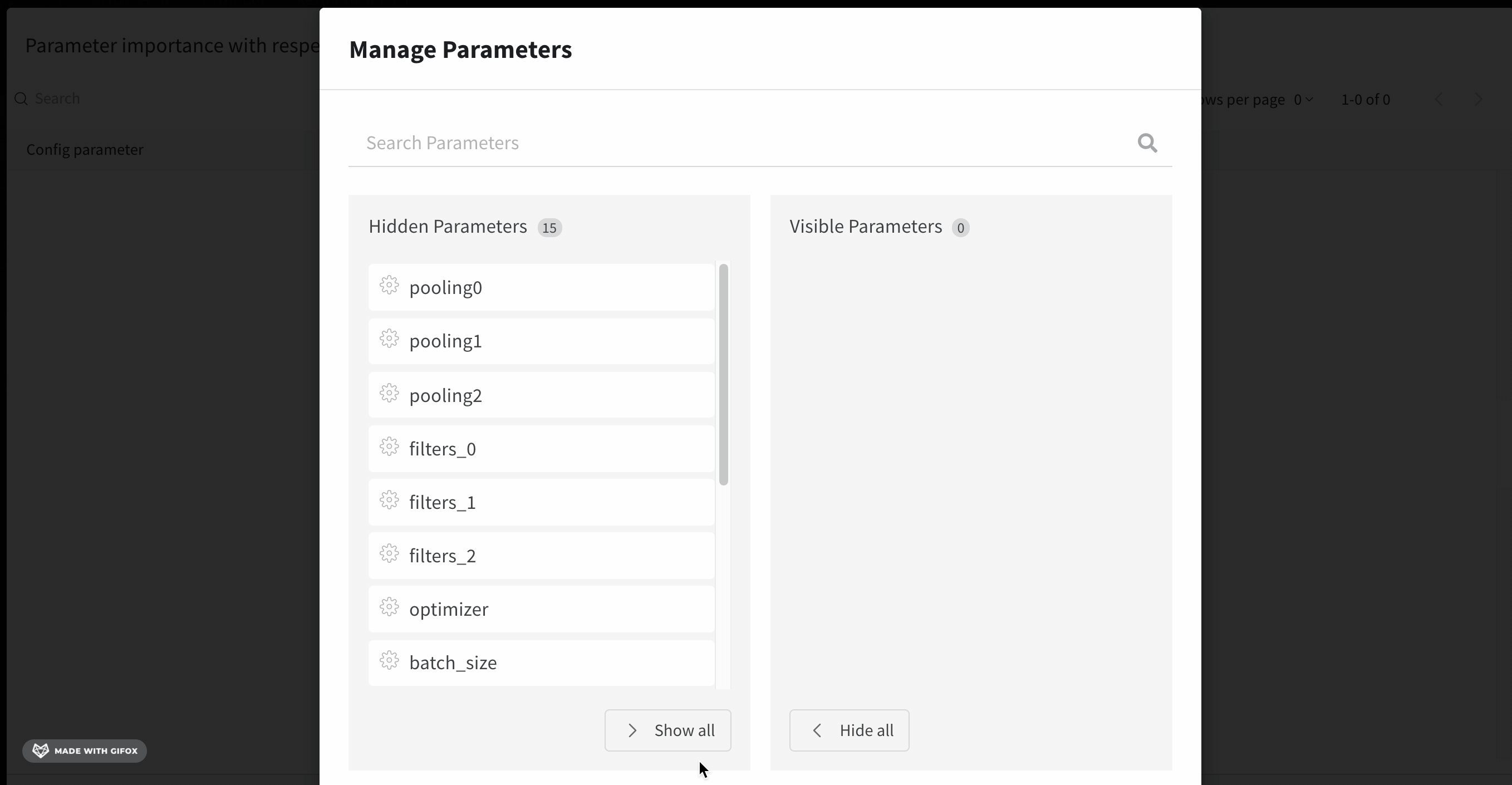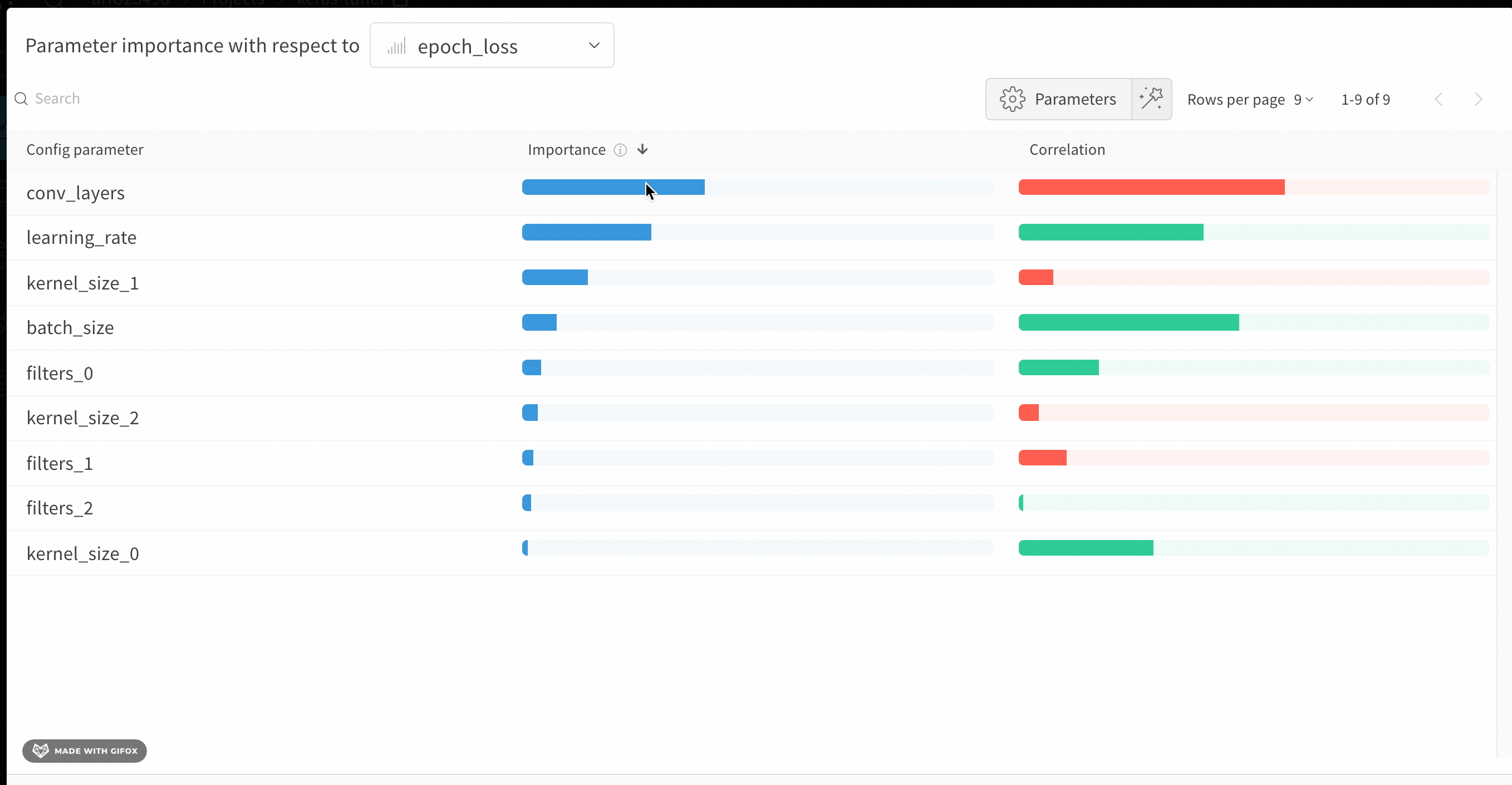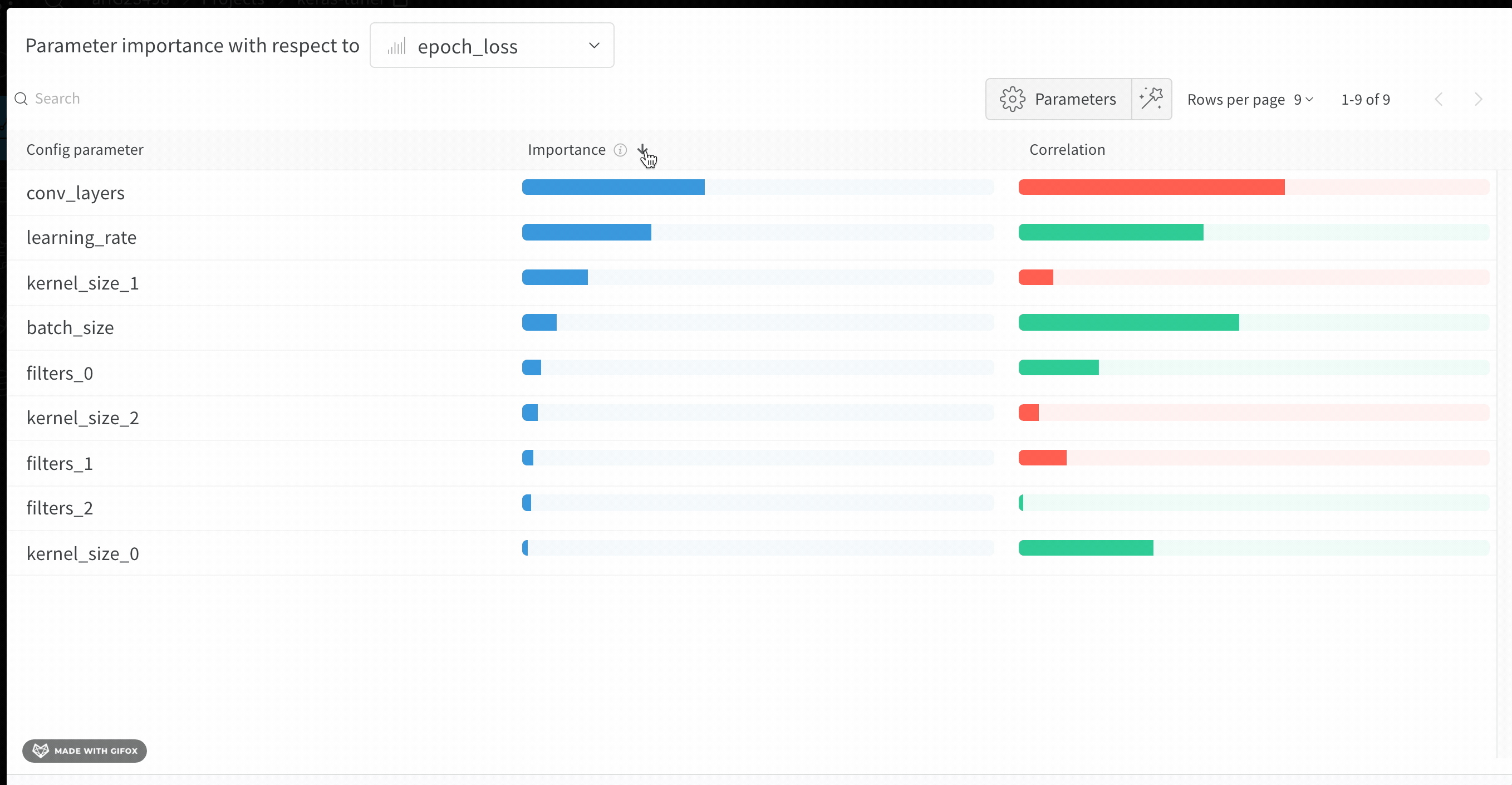
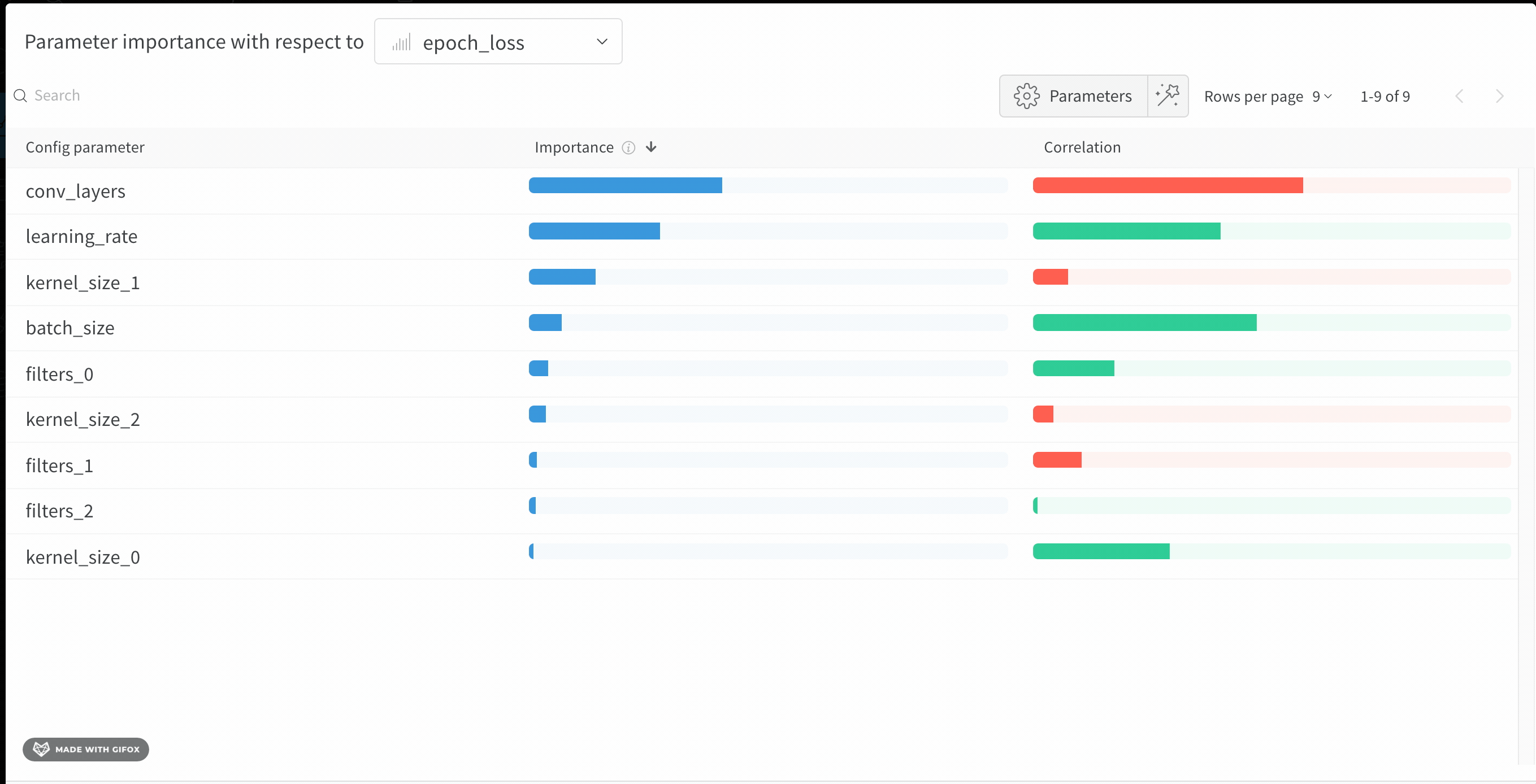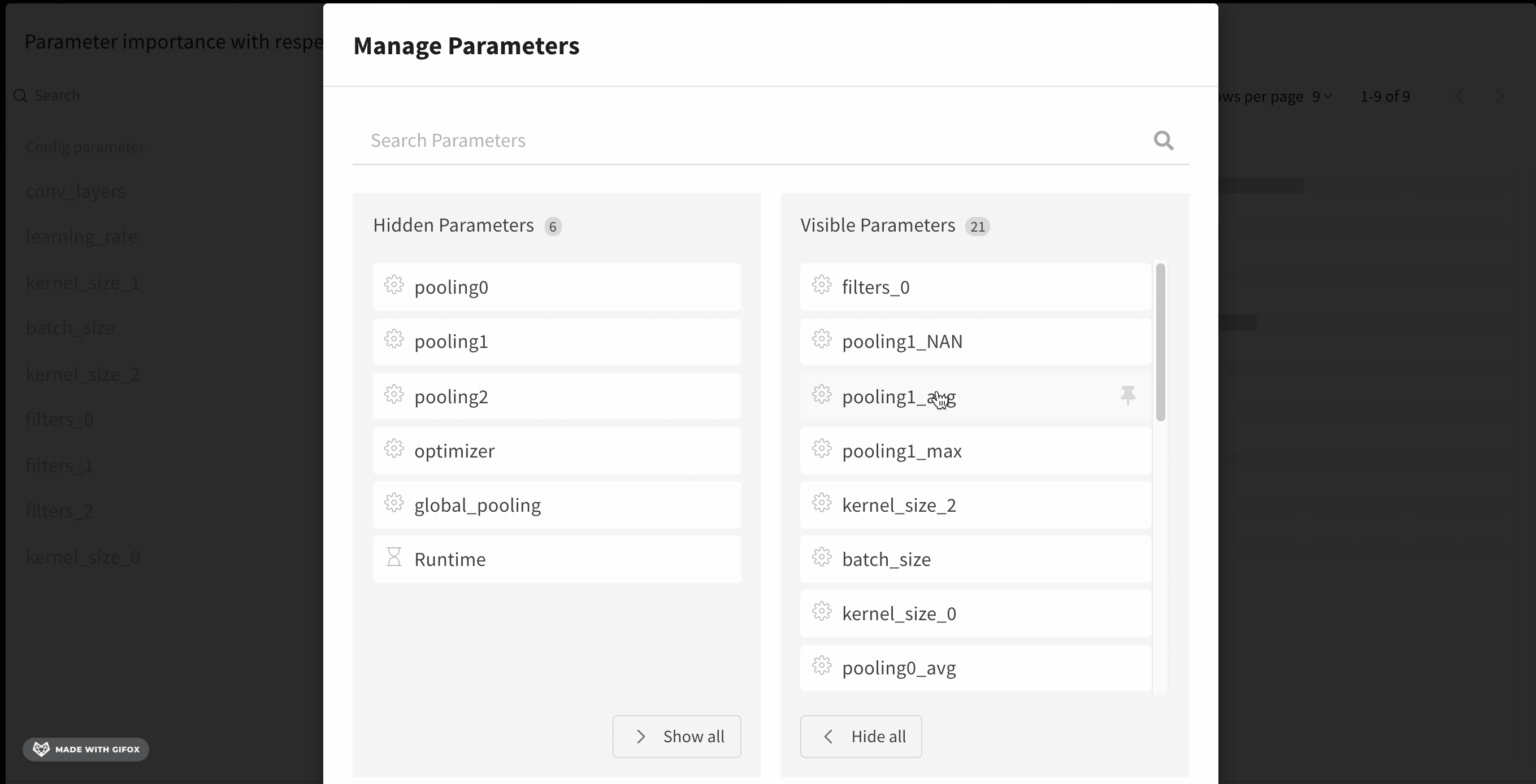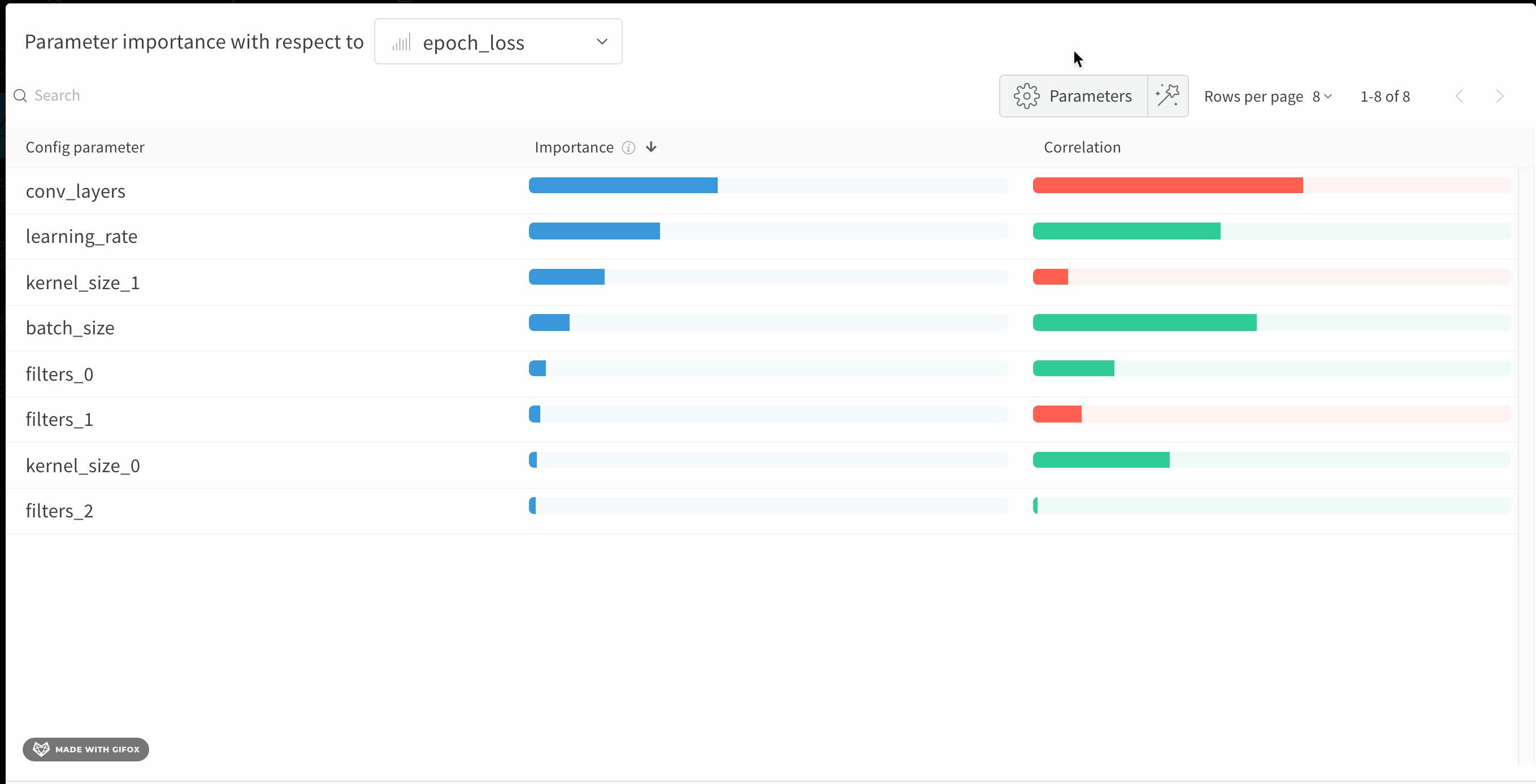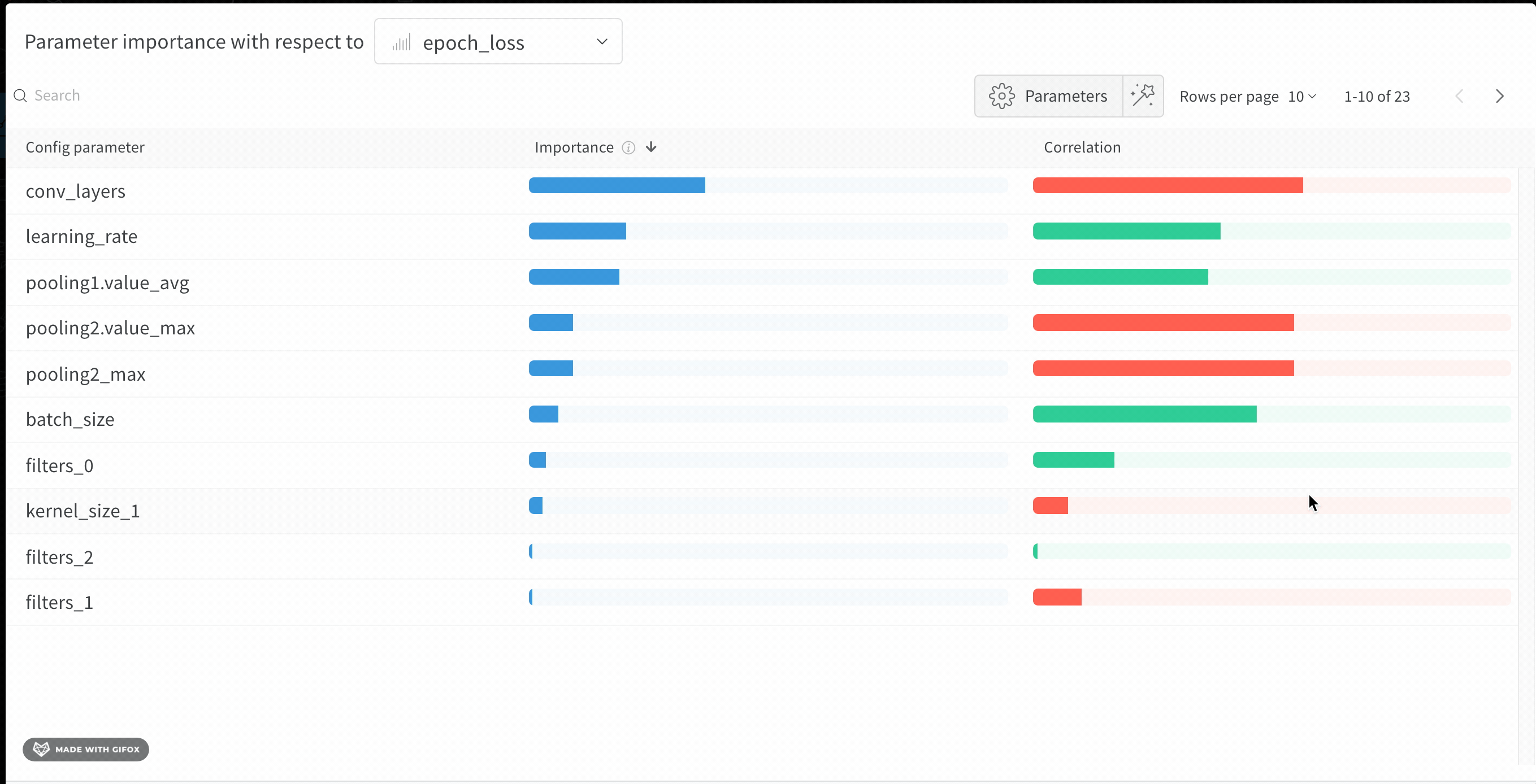
This panel shows you all the parameters passed to the wandb.config object in your training script. Next, it shows the feature importances and correlations of these config parameters with respect to the model metric you select (val_loss in this case).
Importance
The importance column shows you the degree to which each hyperparameter was useful in predicting the chosen metric. We can imagine a scenario in which we start by tuning a plethora of hyperparameters and using this plot to hone in on which ones merit further exploration. The subsequent sweeps can then be limited to the most important hyperparameters, thereby finding a better model faster and cheaper.
Note: We calculate these importances using a tree based model rather than a linear model as the former are more tolerant of both categorical data and data that’s not normalized.\
In the aforementioned panel we can see that epochs, learning_rate, batch_size and weight_decay were fairly important.
As a next step, we might run another sweep exploring more fine grained values of these hyperparameters. Interestingly, while learning_rate and batch_size were important, they weren’t very well correlated to the output.\
This brings us to correlations.
Correlations
Correlations capture linear relationships between individual hyperparameters and metric values. They answer the question – is there a significant relationship between using a hyperparameter, say the SGD optimizer, and my val_loss (the answer in this case is yes). Correlation values range from -1 to 1, where positive values represent positive linear correlation, negative values represent negative linear correlation and a value of 0 represents no correlation. Generally a value greater than 0.7 in either direction represents strong correlation.
We might use this graph to further explore the values that are have a higher correlation to our metric (in this case we might pick stochastic gradient descent or adam over rmsprop or nadam) or train for more epochs.
Quick note on interpreting correlations:
- correlations show evidence of association, not necessarily causation.
- correlations are sensitive to outliers, which might turn a strong relationship to a moderate one, specially if the sample size of hyperparameters tried is small.
- and finally, correlations only capture linear relationships between hyperparameters and metrics. If there is a strong polynomial relationship, it won’t be captured by correlations.
The disparities between importance and correlations result from the fact that importance accounts for interactions between hyperparameters, whereas correlation only measures the affects of individual hyperparameters on metric values. Secondly, correlations capture only the linear relationships, whereas importances can capture more complex ones.
As you can see both importance and correlations are powerful tools for understanding how your hyperparameters influence model performance.
We hope that this panel helps you capture these insights and hone in on a powerful model faster.